Modeling of the thickness of the sensor#
In this notebook we will re-use the experiment done at ID28 and previously calibrated and model in 3D the detector.
This detector is a Pilatus 1M with a 450µm thick silicon sensor. Let’s first have a look at the absorption coefficients of this sensor material:
Reference absorption coeficients are available from: https://physics.nist.gov/PhysRefData/XrayMassCoef/ElemTab/z14.html
First we retieve the results of the previous step, then calculate the absorption efficiency:
%matplotlib inline
# use `widget` instead of `inline` for better user-experience. `inline` allows to store plots into notebooks.
import time
import os
from matplotlib.pyplot import subplots
import numpy
from scipy.sparse import save_npz
import pyFAI
import pyFAI.units
import pyFAI.detectors
from pyFAI.detectors.sensors import Si_MATERIAL
import json
from scipy.sparse import csr_matrix, linalg
try:
import cpuinfo
except ImportError:
cpu = ""
else:
cpu = cpuinfo.cpuinfo.get_cpu_info().get("brand_raw")
start_time = time.perf_counter()
print(f"Using pyFAI vesrion: {pyFAI.version} on a {cpu} with {os.cpu_count()} threads")
with open("id28.json") as f:
calib = json.load(f)
thickness = 450e-6
wavelength = calib["wavelength"]
dist = calib["param"][calib["param_names"].index("dist")]
poni1 = calib["param"][calib["param_names"].index("poni1")]
poni2 = calib["param"][calib["param_names"].index("poni2")]
energy = pyFAI.units.hc / (wavelength * 1e10)
print(f"wavelength: {wavelength:.3e}m,\t "
f"dist: {dist:.3e}m,\t "
f"poni1: {poni1:.3e}m,\t "
f"poni2: {energy:.3e}m,\t "
f"energy: {energy:.3f}keV")
mask = numpy.load("mask.npy").astype(numpy.int8)
Using pyFAI vesrion: 2025.10.0-dev0 on a AMD Ryzen Threadripper PRO 3975WX 32-Cores with 64 threads
wavelength: 6.968e-11m, dist: 2.845e-01m, poni1: 8.865e-02m, poni2: 1.779e+01m, energy: 17.793keV
Absorption coefficient at 17.8 keV#
print(
f"µ = {Si_MATERIAL.mu(energy, unit='cm'):.1f} cm^-1 "
f"hence absorption efficiency for 450µm: {100 * Si_MATERIAL.absorbance(energy, thickness):.1f} %"
)
mu = Si_MATERIAL.mu(energy, unit="m")
µ = 16.4 cm^-1 hence absorption efficiency for 450µm: 52.3 %
from pyFAI.detectors.sensors import Si_MATERIAL
depth = numpy.linspace(0, 1000, 100)
res = [1 - Si_MATERIAL.absorbance(energy, d, "µm") for d in depth]
fig, ax = subplots()
ax.plot(depth, res, "-")
ax.set_xlabel("Depth (µm)")
ax.set_ylabel("Residual signal")
ax.set_title(f"Silicon @ {energy:.1} keV");
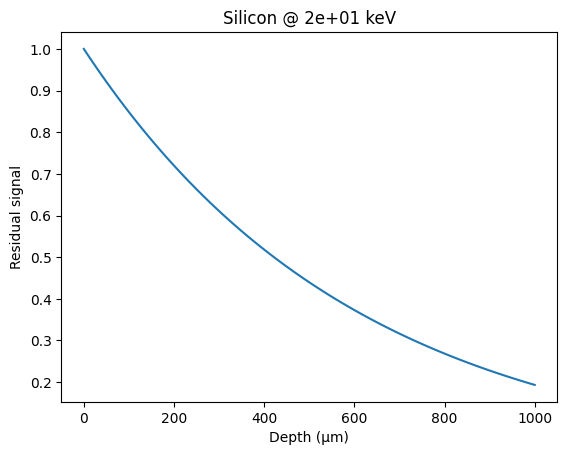
This is consistent with: henke.lbl.gov or web-docs.gsi.de
Now we can model the detector
Modeling of the detector:#
The detector is represented as a 2D array of voxels. Let vox, voy, and voz denote the dimensions of the detector along the three axes.
detector = pyFAI.detector_factory(calib["detector"])
print(detector)
vox = detector.pixel2 # this is not a typo
voy = detector.pixel1 # x <--> axis 2
voz = thickness
print(f"Voxel size: (x:{vox}, y:{voy}, z:{voz})")
Detector Pilatus 1M PixelSize= 172µm, 172µm BottomRight(3)
Voxel size: (x:0.000172, y:0.000172, z:0.00045)
The intensity grabbed in this voxel is the triple integral of the absorbed signal coming from this pixel or from the neighboring ones.
There are 3 ways to perform this intergral:
Volumetric analytic integral. Looks feasible with a change of variable in the depth
Slice per slice, the remaining intensity depand on the incidence angle + pixel splitting between neighbooring pixels
raytracing: the decay can be solved analytically for each ray, one has to throw many ray to average out the signal.
For sake of simplicity, this integral will be calculated numerically using this raytracing algorithm. http://www.cse.yorku.ca/~amana/research/grid.pdf
Knowing the input position for a X-ray on the detector and its propagation vector, this algorithm allows us to calculate the length of the path in all voxel it crosses in a fairly efficient way.
To speed up the calculation, we will use a few tricks:
One ray never crosses more than 16 pixels, which is reasonable considering the incidance angle
we use numba to speed-up the calculation of loops in python
We will allocate the needed memory by chuncks of 1 million elements
! pip install numba cython
Requirement already satisfied: numba in /users/kieffer/.venv/py313/lib/python3.13/site-packages (0.62.1)
Requirement already satisfied: cython in /users/kieffer/.venv/py313/lib/python3.13/site-packages (3.0.12)
Requirement already satisfied: llvmlite<0.46,>=0.45.0dev0 in /users/kieffer/.venv/py313/lib/python3.13/site-packages (from numba) (0.45.1)
Requirement already satisfied: numpy<2.4,>=1.22 in /users/kieffer/.venv/py313/lib/python3.13/site-packages (from numba) (2.3.1)
Raytracing using numba#
BLOCK_SIZE = 1 << 20 # 1 million
BUFFER_SIZE = 16
BIG = numpy.finfo(numpy.float32).max
Now that we are able to perform raytracing for any ray entering the detector, we can calculate the contribution to the neighboring pixels, using the absorption law (the length traveled is already known). To average-out the signal, we will sample a few dozens of rays per pixel to get an approximation of the volume integral.
Now we need to store the results so that this transformation can be represented as a sparse matrix multiplication:
b = M.a
Where b is the recorded image (blurred) and a is the “perfect” signal. M being the sparse matrix where every pixel of a gives a limited number of contribution to b.
Each pixel in b is represented by one line in M and we store the indices of a of interest with the coefficients of the matrix. So if a pixel i,j contributes to (i,j), (i+1,j), (i+1,j+1), there are only 3 elements in the line. This is advantageous for storage.
We will use the CSR sparse matrix representation: https://en.wikipedia.org/wiki/Sparse_matrix#Compressed_sparse_row_.28CSR.2C_CRS_or_Yale_format.29 where there are 3 arrays:
data: containing the actual non zero values
indices: for a given line, it contains the column number of the associated data (at the same indice)
idptr: this array contains the index of the start of every line.
from numba.experimental import jitclass
from numba import int8, int32, int64, float32, float64
spec = [
("vox", float64),
("voy", float64),
("voz", float64),
("mu", float64),
("dist", float64),
("poni1", float64),
("poni2", float64),
("width", int64),
("height", int64),
("mask", int8[:, :]),
("sampled", int64),
("data", float32[:]),
("indices", int32[:]),
("idptr", int32[:]),
]
@jitclass(spec)
class ThickDetector(object):
"Calculate the point spread function as function of the geometry of the experiment"
def __init__(self, vox, voy, thickness, mask, mu, dist, poni1, poni2):
"""Constructor of the class:
:param vox, voy: detector pixel size in the plane
:param thickness: thickness of the sensor in meters
:param mask:
:param mu: absorption coefficient of the sensor material
:param dist: sample detector distance as defined in the geometry-file
:param poni1, poni2: coordinates of the PONI as defined in the geometry
"""
self.vox = vox
self.voy = voy
self.voz = thickness
self.mu = mu
self.dist = dist
self.poni1 = poni1
self.poni2 = poni2
self.width = mask.shape[-1]
self.height = mask.shape[0]
self.mask = mask
self.sampled = 0
self.data = numpy.zeros(BLOCK_SIZE, dtype=numpy.float32)
self.indices = numpy.zeros(BLOCK_SIZE, dtype=numpy.int32)
self.idptr = numpy.zeros(self.width * self.height + 1, dtype=numpy.int32)
def calc_one_ray(self, entx, enty):
"""For a ray entering at position (entx, enty), with a propagation vector (kx, ky,kz),
calculate the length spent in every voxel where energy is deposited from a bunch of photons entering the detector
at a given position and and how much energy they deposit in each voxel.
Direct implementation of http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.42.3443&rep=rep1&type=pdf
:param entx, enty: coordinate of the entry point in meter (2 components, x,y)
:return: coordinates voxels in x, y and length crossed when leaving the associated voxel
"""
array_x = numpy.empty(BUFFER_SIZE, dtype=numpy.int32)
array_x[:] = -1
array_y = numpy.empty(BUFFER_SIZE, dtype=numpy.int32)
array_y[:] = -1
array_len = numpy.empty(BUFFER_SIZE, dtype=numpy.float32)
# normalize the input propagation vector
kx = entx - self.poni2
ky = enty - self.poni1
kz = self.dist
n = numpy.sqrt(kx * kx + ky * ky + kz * kz)
kx /= n
ky /= n
kz /= n
step_X = -1 if kx < 0.0 else 1
step_Y = -1 if ky < 0.0 else 1
X = int(entx / self.vox)
Y = int(enty / self.voy)
if kx > 0.0:
t_max_x = ((entx // self.vox + 1) * (self.vox) - entx) / kx
elif kx < 0.0:
t_max_x = ((entx // self.vox) * (self.vox) - entx) / kx
else:
t_max_x = BIG
if ky > 0.0:
t_max_y = ((enty // self.voy + 1) * (self.voy) - enty) / ky
elif ky < 0.0:
t_max_y = ((enty // self.voy) * (self.voy) - enty) / ky
else:
t_max_y = BIG
# Only one case for z as the ray is travelling in one direction only
t_max_z = self.voz / kz
t_delta_x = abs(self.vox / kx) if kx != 0 else BIG
t_delta_y = abs(self.voy / ky) if ky != 0 else BIG
t_delta_z = self.voz / kz
finished = False
last_id = 0
array_x[last_id] = X
array_y[last_id] = Y
while not finished:
if t_max_x < t_max_y:
if t_max_x < t_max_z:
array_len[last_id] = t_max_x
last_id += 1
X += step_X
array_x[last_id] = X
array_y[last_id] = Y
t_max_x += t_delta_x
else:
array_len[last_id] = t_max_z
last_id += 1
finished = True
else:
if t_max_y < t_max_z:
array_len[last_id] = t_max_y
last_id += 1
Y += step_Y
array_x[last_id] = X
array_y[last_id] = Y
t_max_y += t_delta_y
else:
array_len[last_id] = t_max_z
last_id += 1
finished = True
if last_id >= array_len.size - 1:
print("resize arrays")
old_size = len(array_len)
new_size = (old_size // BUFFER_SIZE + 1) * BUFFER_SIZE
new_array_x = numpy.empty(new_size, dtype=numpy.int32)
new_array_x[:] = -1
new_array_y = numpy.empty(new_size, dtype=numpy.int32)
new_array_y[:] = -1
new_array_len = numpy.empty(new_size, dtype=numpy.float32)
new_array_x[:old_size] = array_x
new_array_y[:old_size] = array_y
new_array_len[:old_size] = array_len
array_x = new_array_x
array_y = new_array_y
array_len = new_array_len
return array_x[:last_id], array_y[:last_id], array_len[:last_id]
def one_pixel(self, row, col, sample):
"""calculate the contribution of one pixel to the sparse matrix and populate it.
:param row: row index of the pixel of interest
:param col: column index of the pixel of interest
:param sample: Oversampling rate, 10 will cast 10x10 ray per pixel
:return: the extra number of pixel allocated
"""
if self.mask[row, col]:
return (
numpy.empty(0, dtype=numpy.int32),
numpy.empty(0, dtype=numpy.float32),
)
counter = 0
tmp_size = 0
last_buffer_size = BUFFER_SIZE
tmp_idx = numpy.empty(last_buffer_size, dtype=numpy.int32)
tmp_idx[:] = -1
tmp_coef = numpy.zeros(last_buffer_size, dtype=numpy.float32)
pos = row * self.width + col
start = self.idptr[pos]
for i in range(sample):
posx = (col + 1.0 * i / sample) * vox
for j in range(sample):
posy = (row + 1.0 * j / sample) * voy
array_x, array_y, array_len = self.calc_one_ray(posx, posy)
rem = 1.0
for i in range(array_x.size):
x = array_x[i]
y = array_y[i]
l = array_len[i]
if (x < 0) or (y < 0) or (y >= self.height) or (x >= self.width):
break
elif self.mask[y, x]:
continue
idx = x + y * self.width
dos = numpy.exp(-self.mu * l)
value = rem - dos
rem = dos
for j in range(last_buffer_size):
if tmp_size >= last_buffer_size:
# Increase buffer size
new_buffer_size = last_buffer_size + BUFFER_SIZE
new_idx = numpy.empty(new_buffer_size, dtype=numpy.int32)
new_coef = numpy.zeros(new_buffer_size, dtype=numpy.float32)
new_idx[:last_buffer_size] = tmp_idx
new_idx[last_buffer_size:] = -1
new_coef[:last_buffer_size] = tmp_coef
last_buffer_size = new_buffer_size
tmp_idx = new_idx
tmp_coef = new_coef
if tmp_idx[j] == idx:
tmp_coef[j] += value
break
elif tmp_idx[j] < 0:
tmp_idx[j] = idx
tmp_coef[j] = value
tmp_size += 1
break
return tmp_idx[:tmp_size], tmp_coef[:tmp_size]
def calc_csr(self, sample):
"""Calculate the CSR matrix for the whole image
:param sample: Oversampling factor
:return: CSR matrix
"""
size = self.width * self.height
allocated_size = BLOCK_SIZE
idptr = numpy.zeros(size + 1, dtype=numpy.int32)
indices = numpy.zeros(allocated_size, dtype=numpy.int32)
data = numpy.zeros(allocated_size, dtype=numpy.float32)
self.sampled = sample * sample
pos = 0
start = 0
for row in range(self.height):
for col in range(self.width):
line_idx, line_coef = self.one_pixel(row, col, sample)
line_size = line_idx.size
if line_size == 0:
new_size = 0
pos += 1
idptr[pos] = start
continue
stop = start + line_size
if stop >= allocated_size:
new_buffer_size = allocated_size + BLOCK_SIZE
new_idx = numpy.zeros(new_buffer_size, dtype=numpy.int32)
new_coef = numpy.zeros(new_buffer_size, dtype=numpy.float32)
new_idx[:allocated_size] = indices
new_coef[:allocated_size] = data
allocated_size = new_buffer_size
indices = new_idx
data = new_coef
indices[start:stop] = line_idx
data[start:stop] = line_coef
pos += 1
idptr[pos] = stop
start = stop
last = idptr[-1]
self.data = data
self.indices = indices
self.idptr = idptr
return (self.data[:last] / self.sampled, indices[:last], idptr)
nbthick = ThickDetector(
vox, voy, thickness=thickness, mu=mu, dist=dist, poni1=poni1, poni2=poni2, mask=mask
)
%time nbthick.calc_csr(1)
CPU times: user 3.95 s, sys: 236 ms, total: 4.19 s
Wall time: 4.2 s
(array([0., 0., 0., ..., 0., 0., 0.], shape=(1902583,), dtype=float32),
array([ 2, 2, 4, ..., 1023180, 1023181, 1023182],
shape=(1902583,), dtype=int32),
array([ 0, 0, 0, ..., 1902581, 1902582, 1902583],
shape=(1023184,), dtype=int32))
%time nbthick.calc_csr(4)
CPU times: user 3.68 s, sys: 7.78 ms, total: 3.69 s
Wall time: 3.68 s
(array([0.17449115, 0.10933631, 0.17465518, ..., 0.24611568, 0.03161056,
0.24604346], shape=(3410359,), dtype=float32),
array([ 2, 2, 3, ..., 1023181, 1023182, 1023182],
shape=(3410359,), dtype=int32),
array([ 0, 0, 0, ..., 3410356, 3410358, 3410359],
shape=(1023184,), dtype=int32))
Same implementation using Cython#
Cython is an ahead of time compiler for Python code. Thus it requires a compiler (gcc, msvc, …) needs to be installed on your computer and available. This is usually already the case under linux but requires some work under windows or macos.
%load_ext Cython
%%cython --compile-args=-fopenmp --link-args=-fopenmp
#cython: embedsignature=True, language_level=3, binding=True
#cython: boundscheck=False, wraparound=False, cdivision=True, initializedcheck=False,
## This is for developping:
## cython: profile=True, warn.undeclared=True, warn.unused=True, warn.unused_result=False, warn.unused_arg=True
##
import cython
import numpy
from libc.math cimport sqrt, exp
from cython.parallel import prange
from libc.stdint cimport int8_t, uint8_t, int16_t, uint16_t, \
int32_t, uint32_t, int64_t, uint64_t
ctypedef double float64_t
ctypedef float float32_t
cdef int32_t BUFFER_SIZE = 16
cdef float64_t BIG = numpy.finfo(numpy.float32).max
cdef class CythonThickDetector:
"Calculate the point spread function as function of the geometry of the experiment"
cdef:
public float64_t vox
public float64_t voy
public float64_t voz
public float64_t mu
public float64_t dist
public float64_t poni1
public float64_t poni2
public int oversampling
public int buffer_size
public int width
public int height
public int size
public int8_t[:, ::1] mask
def __init__(self,
float64_t vox,
float64_t voy,
float64_t thickness,
mask,
float64_t mu,
float64_t dist,
float64_t poni1,
float64_t poni2,
int buffer_size=BUFFER_SIZE):
"""Constructor of the class:
:param vox, voy: detector pixel size in the plane
:param thickness: thickness of the sensor in meters
:param mask:
:param mu: absorption coefficient of the sensor material
:param dist: sample detector distance as defined in the geometry-file
:param poni1, poni2: coordinates of the PONI as defined in the geometry
"""
self.vox = float(vox)
self.voy = float(voy)
self.voz = float(thickness)
self.mu = float(mu)
self.dist = float(dist)
self.poni1 = float(poni1)
self.poni2 = float(poni2)
self.width = int(mask.shape[1])
self.height = int(mask.shape[0])
self.size = self.width*self.height
self.mask = numpy.ascontiguousarray(mask, numpy.int8)
self.oversampling = 1
self.buffer_size = int(buffer_size)
def calc_one_ray(self, entx, enty):
"""For a ray entering at position (entx, enty), with a propagation vector (kx, ky,kz),
calculate the length spent in every voxel where energy is deposited from a bunch of photons entering the detector
at a given position and and how much energy they deposit in each voxel.
Direct implementation of http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.42.3443&rep=rep1&type=pdf
:param entx, enty: coordinate of the entry point in meter (2 components, x,y)
:return: coordinates voxels in x, y and length crossed when leaving the associated voxel
"""
cdef:
int last_id
float64_t _entx = float(entx)
float64_t _enty = float(enty)
int32_t[::1] array_x = numpy.empty(self.buffer_size, dtype=numpy.int32)
int32_t[::1] array_y = numpy.empty(self.buffer_size, dtype=numpy.int32)
float32_t[::1] array_len = numpy.empty(self.buffer_size, dtype=numpy.float32)
with nogil:
last_id = self._calc_one_ray(_entx, _enty,
array_x, array_y, array_len)
if last_id>self.buffer_size:
raise RuntimeError(f"Temporary buffer size ({last_id}) larger than expected ({self.buffer_size})")
return (numpy.asarray(array_x[:last_id]),
numpy.asarray(array_y[:last_id]),
numpy.asarray(array_len[:last_id]))
cdef int _calc_one_ray(self,
float64_t entx,
float64_t enty,
int32_t[::1] array_x,
int32_t[::1] array_y,
float32_t[::1] array_len
)noexcept nogil:
"""Return number of entries in the array_x[:last_id], array_y[:last_id], array_len[:last_id]"""
cdef:
float64_t kx, ky, kz, n, t_max_x, t_max_y, t_max_z, t_delta_x, t_delta_y#, t_delta_z
int step_X, step_Y, X, Y, last_id
bint finished
# reset arrays
array_x[:] = -1
array_y[:] = -1
array_len[:] = 0.0
# normalize the input propagation vector
kx = entx - self.poni2
ky = enty - self.poni1
kz = self.dist
n = sqrt(kx*kx + ky*ky + kz*kz)
kx /= n
ky /= n
kz /= n
step_X = -1 if kx<0.0 else 1
step_Y = -1 if ky<0.0 else 1
X = int(entx/self.vox)
Y = int(enty/self.voy)
if kx>0.0:
t_max_x = ((entx//self.vox+1)*(self.vox)-entx)/ kx
elif kx<0.0:
t_max_x = ((entx//self.vox)*(self.vox)-entx)/ kx
else:
t_max_x = BIG
if ky>0.0:
t_max_y = ((enty//self.voy+1)*(self.voy)-enty)/ ky
elif ky<0.0:
t_max_y = ((enty//self.voy)*(self.voy)-enty)/ ky
else:
t_max_y = BIG
#Only one case for z as the ray is travelling in one direction only
t_max_z = self.voz / kz
t_delta_x = abs(self.vox/kx) if kx!=0 else BIG
t_delta_y = abs(self.voy/ky) if ky!=0 else BIG
# t_delta_z = self.voz/kz
finished = False
last_id = 0
array_x[last_id] = X
array_y[last_id] = Y
while not finished:
if t_max_x < t_max_y:
if t_max_x < t_max_z:
array_len[last_id] = t_max_x
last_id = last_id + 1
X = X + step_X
array_x[last_id] = X
array_y[last_id] = Y
t_max_x = t_max_x + t_delta_x
else:
array_len[last_id] = t_max_z
last_id = last_id + 1
finished = True
else:
if t_max_y < t_max_z:
array_len[last_id] = t_max_y
last_id = last_id +1
Y = Y + step_Y
array_x[last_id] = X
array_y[last_id] = Y
t_max_y = t_max_y + t_delta_y
else:
array_len[last_id] = t_max_z
last_id = last_id +1
finished = True
if last_id>=self.buffer_size:
return self.buffer_size
return last_id
def one_pixel(self, row, col, sample=0):
"""calculate the contribution of one pixel to the sparse matrix and populate it.
:param row: row index of the pixel of interest
:param col: column index of the pixel of interest
:param sample: Oversampling rate, 10 will cast 10x10 ray per pixel
"""
cdef:
int entries = 0
int _row = int(row)
int _col = int(col)
int32_t[::1] tmp_idx = numpy.empty(self.buffer_size, dtype=numpy.int32)
float32_t[::1] tmp_coef = numpy.empty(self.buffer_size, dtype=numpy.float32)
int32_t[::1] array_x = numpy.empty(self.buffer_size, dtype=numpy.int32)
int32_t[::1] array_y = numpy.empty(self.buffer_size, dtype=numpy.int32)
float32_t[::1] array_len = numpy.empty(self.buffer_size, dtype=numpy.float32)
if sample:
self.oversampling = sample
with nogil:
entries = self._one_pixel(_row, _col, tmp_idx, tmp_coef, array_x, array_y, array_len)
if entries<self.buffer_size:
return (numpy.asarray(tmp_idx)[:entries],numpy.asarray(tmp_coef)[:entries])
else:
raise RuntimeError(f"Pixel produced {entries} voxels, limited to {self.buffer_size}. Increase Buffer size ! in constructor")
cdef int _one_pixel(self, int row, int col,
int32_t[::1] tmp_idx,
float32_t[::1] tmp_coef,
int32_t[::1] array_x,
int32_t[::1] array_y,
float32_t[::1] array_len
)noexcept nogil:
"return the number of elements in tmp_idx/tmp_coef which are to be used"
cdef:
int i, j, tmp_size, last_buffer_size, n, x, y, idx
float64_t rem, l, posx, posy, value, dos
if self.mask[row, col]:
return 0
tmp_size = 0
last_buffer_size = tmp_idx.shape[0]
tmp_idx[:] = -1
tmp_coef[:] = 0.0
for i in range(self.oversampling):
posx = (col+1.0*i/self.oversampling)*self.vox
for j in range(self.oversampling):
posy = (row+1.0*j/self.oversampling)*self.voy
n = self._calc_one_ray(posx, posy, array_x, array_y, array_len)
rem = 1.0
for i in range(min(n, self.buffer_size)):
x = array_x[i]
y = array_y[i]
l = array_len[i]
if (x<0) or (y<0) or (y>=self.height) or (x>=self.width):
break
elif (self.mask[y, x]):
continue
idx = x + y*self.width
dos = exp(-self.mu*l)
value = rem - dos
rem = dos
for j in range(self.buffer_size):
if tmp_idx[j] == idx:
tmp_coef[j] = tmp_coef[j] + value
break
elif tmp_idx[j] < 0:
tmp_idx[j] = idx
tmp_coef[j] = value
tmp_size = tmp_size + 1
break
if tmp_size >= self.buffer_size:
break
return tmp_size
def calc_csr(self, sample=0, int threads=0):
"""Calculate the content of the sparse matrix for the whole image
:param sample: Oversampling factor
:param threads: number of threads to be used
:return: spase matrix?
"""
cdef:
int pos, i, current, next, size
int32_t[::1] sizes, indptr = numpy.zeros(self.size+1, dtype=numpy.int32)
int32_t[:, ::1] indices
float32_t[:, ::1] data
int32_t[::1] csr_indices
float32_t[::1] csr_data
int32_t[:, ::1] array_x
int32_t[:, ::1] array_y
float32_t[:, ::1] array_len
if sample:
self.oversampling = sample
self.oversampling = sample
data = numpy.zeros((self.size, self.buffer_size), dtype=numpy.float32)
indices = numpy.zeros((self.size, self.buffer_size),dtype=numpy.int32)
sizes = numpy.zeros(self.size, dtype=numpy.int32)
#single threaded version:
array_x = numpy.empty((self.size, self.buffer_size), dtype=numpy.int32)
array_y = numpy.empty((self.size, self.buffer_size), dtype=numpy.int32)
array_len = numpy.empty((self.size, self.buffer_size), dtype=numpy.float32)
for pos in prange(self.size, num_threads=threads, nogil=True):
size = sizes[pos] = self._one_pixel(pos//self.width, pos%self.width,
indices[pos], data[pos],
array_x[pos], array_y[pos], array_len[pos])
size = numpy.sum(sizes)
csr_indices = numpy.empty(size, numpy.int32)
csr_data = numpy.empty(size, numpy.float32)
current = 0
for i in range(self.size):
size = sizes[i]
next = current + size
indptr[i+1] = next
csr_indices[current:next] = indices[i,:size]
csr_data[current:next] = data[i,:size]
current = next
return (numpy.asarray(csr_data)/(self.oversampling*self.oversampling),
numpy.asarray(csr_indices),
numpy.asarray(indptr))
cythick = CythonThickDetector(
172e-6,
172e-6,
thickness=thickness,
mu=mu,
dist=dist,
poni1=poni1,
poni2=poni2,
mask=mask,
)
print("Performance of Cython implementation:")
%time cythick.calc_csr(4, threads=1)
Performance of Cython implementation:
CPU times: user 1.01 s, sys: 47.9 ms, total: 1.05 s
Wall time: 1.05 s
(array([0.17449115, 0.10933631, 0.17465518, ..., 0.35667214, 0.05905784,
0.35653958], shape=(3328700,), dtype=float32),
array([ 2, 2, 3, ..., 1023181, 1023182, 1023182],
shape=(3328700,), dtype=int32),
array([ 0, 0, 0, ..., 3328697, 3328699, 3328700],
shape=(1023184,), dtype=int32))
# Comparison with Numba, Cython is usually slightly faster
print("Performance of Numba implementation:")
%time nbthick.calc_csr(4)
Performance of Numba implementation:
CPU times: user 3.65 s, sys: 28 ms, total: 3.68 s
Wall time: 3.67 s
(array([0.17449115, 0.10933631, 0.17465518, ..., 0.24611568, 0.03161056,
0.24604346], shape=(3410359,), dtype=float32),
array([ 2, 2, 3, ..., 1023181, 1023182, 1023182],
shape=(3410359,), dtype=int32),
array([ 0, 0, 0, ..., 3410356, 3410358, 3410359],
shape=(1023184,), dtype=int32))
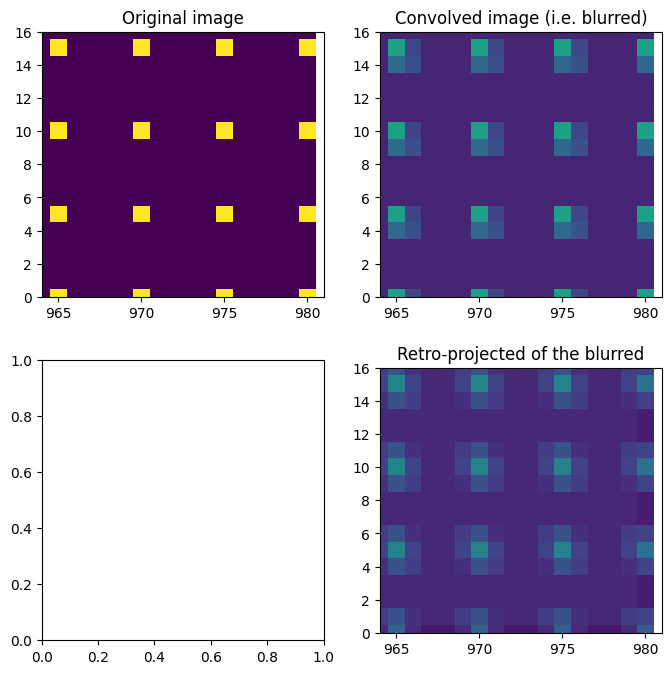
Validation of the CSR matrix obtained:#
For this we will build a simple 2D image with one pixel in a regular grid and calculate the effect of the transformation calculated previously on it.
%time csr = csr_matrix(cythick.calc_csr(10))
CPU times: user 11.1 s, sys: 403 ms, total: 11.5 s
Wall time: 358 ms
dummy_image = numpy.ones(mask.shape, dtype="float32")
dummy_image[::5, ::5] = 10
dummy_blurred = csr.T.dot(dummy_image.ravel()).reshape(mask.shape)
fix, ax = subplots(2, 2, figsize=(8, 8))
ax[0, 0].imshow(dummy_image)
ax[0, 0].set_title("Original image")
ax[0, 1].imshow(dummy_blurred)
ax[0, 1].set_title("Convolved image (i.e. blurred)")
ax[1, 1].imshow(csr.dot(dummy_blurred.ravel()).reshape(mask.shape))
ax[1, 1].set_title("Retro-projected of the blurred")
ax[0, 0].set_xlim(964, 981)
ax[0, 0].set_ylim(0, 16)
ax[0, 1].set_xlim(964, 981)
ax[0, 1].set_ylim(0, 16)
ax[1, 1].set_xlim(964, 981)
ax[1, 1].set_ylim(0, 16);
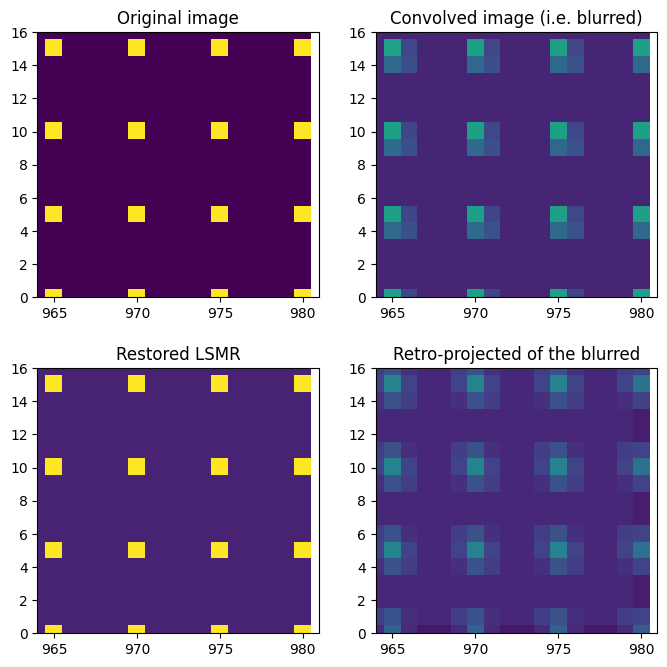
Least squares refinement of the pseudo-inverse#
blured = dummy_blurred.ravel()
# Invert this matrix: see https://arxiv.org/abs/1006.0758
%time res = linalg.lsmr(csr.T, blured)
restored = res[0].reshape(mask.shape)
fix, ax = subplots(2, 2, figsize=(8, 8))
ax[0, 0].imshow(dummy_image)
ax[0, 0].set_title("Original image")
ax[0, 1].imshow(dummy_blurred)
ax[0, 1].set_title("Convolved image (i.e. blurred)")
ax[1, 1].imshow(csr.dot(dummy_blurred.ravel()).reshape(mask.shape))
ax[1, 1].set_title("Retro-projected of the blurred")
ax[0, 0].set_xlim(964, 981)
ax[0, 0].set_ylim(0, 16)
ax[0, 1].set_xlim(964, 981)
ax[0, 1].set_ylim(0, 16)
ax[1, 1].set_xlim(964, 981)
ax[1, 1].set_ylim(0, 16)
ax[1, 0].imshow(restored)
ax[1, 0].set_title("Restored LSMR")
ax[1, 0].set_xlim(964, 981)
ax[1, 0].set_ylim(0, 16);
/users/kieffer/.venv/py313/lib/python3.13/site-packages/scipy/sparse/linalg/_isolve/lsmr.py:407: RuntimeWarning: overflow encountered in cast
condA = max(maxrbar, rhotemp) / min(minrbar, rhotemp)
/users/kieffer/.venv/py313/lib/python3.13/site-packages/scipy/sparse/linalg/_isolve/lsmr.py:406: RuntimeWarning: overflow encountered in cast
minrbar = min(minrbar, rhobarold)
CPU times: user 26.8 s, sys: 4.04 ms, total: 26.8 s
Wall time: 455 ms
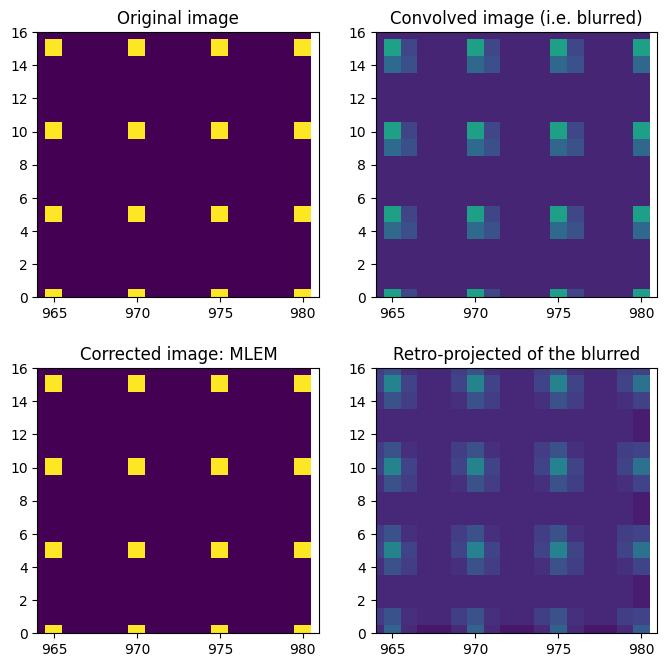
Pseudo inverse with positivitiy constrain and poissonian noise (MLEM)#
The MLEM algorithm was initially developed within the framework of reconstruction of images in emission tomography [Shepp and Vardi, 1982], [Vardi et al., 1985], [Lange and Carson, 1984]. Nowadays, this algorithm is employed in numerous tomographic reconstruction problems and often associated to regularization techniques. It is based on the iterative maximization of the log-likelihood function.
def iterMLEM_scipy(F, M, R):
"Implement one step of MLEM"
# res = F * (R.T.dot(M))/R.dot(F)# / M.sum(axis=-1)
norm = 1 / R.T.dot(numpy.ones_like(F))
cor = R.T.dot(M / R.dot(F))
res = norm * F * cor
res[numpy.isnan(res)] = 1.0
return res
def deconv_MLEM(csr, data, thres=0.2, maxiter=1000):
R = csr.T
msk = data < 0
img = data.astype("float32")
img[msk] = 0.0 # set masked values to 0, negative values could induce errors
M = img.ravel()
# F0 = numpy.random.random(data.size)#M#
F0 = R.T.dot(M)
F1 = iterMLEM_scipy(F0, M, R)
delta = abs(F1 - F0).max()
for i in range(maxiter):
if delta < thres:
break
F2 = iterMLEM_scipy(F1, M, R)
delta = abs(F1 - F2).max()
if i % 100 == 0:
print(i, delta)
F1 = F2
i += 1
print(i, delta)
return F2.reshape(img.shape)
%time res = deconv_MLEM(csr, dummy_blurred, 1e-4)
/tmp/ipykernel_3870469/3638533218.py:4: RuntimeWarning: divide by zero encountered in divide
norm = 1 / R.T.dot(numpy.ones_like(F))
/tmp/ipykernel_3870469/3638533218.py:5: RuntimeWarning: invalid value encountered in divide
cor = R.T.dot(M / R.dot(F))
/tmp/ipykernel_3870469/3638533218.py:6: RuntimeWarning: invalid value encountered in multiply
res = norm * F * cor
0 1.7501588
100 0.0014371872
200 0.00016927719
228 9.930134e-05
CPU times: user 2.66 s, sys: 19.9 ms, total: 2.67 s
Wall time: 2.67 s
fix, ax = subplots(2, 2, figsize=(8, 8))
ax[0, 0].imshow(dummy_image)
ax[0, 1].imshow(dummy_blurred)
ax[1, 1].imshow(csr.dot(dummy_blurred.ravel()).reshape(mask.shape))
ax[0, 0].set_xlim(964, 981)
ax[0, 0].set_ylim(0, 16)
ax[0, 0].set_title("Original image")
ax[0, 1].set_xlim(964, 981)
ax[0, 1].set_ylim(0, 16)
ax[0, 1].set_title("Convolved image (i.e. blurred)")
ax[1, 1].set_xlim(964, 981)
ax[1, 1].set_ylim(0, 16)
ax[1, 1].set_title("Retro-projected of the blurred")
# ax[1,0].set_title("Corrected image");
ax[1, 0].imshow(res)
ax[1, 0].set_xlim(964, 981)
ax[1, 0].set_ylim(0, 16)
ax[1, 0].set_title("Corrected image: MLEM");
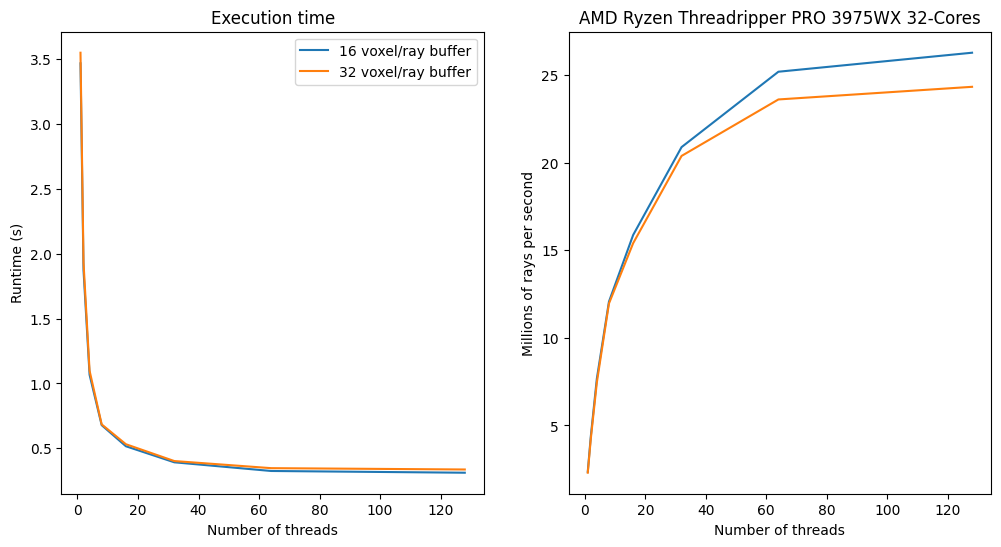
Performance measurements … multi-threaded#
perfs = {}
for i in range(8):
j = 1 << i
print(f"{j:3d} threads: ", end="")
perfs[(j, cythick.buffer_size)] = %timeit -o -n1 -r1 cythick.calc_csr(8, threads=j)
1 threads: 3.47 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
2 threads: 1.87 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
4 threads: 1.07 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
8 threads: 679 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
16 threads: 516 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
32 threads: 392 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
64 threads: 325 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
128 threads: 312 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
buf = 32
cythick = CythonThickDetector(
172e-6,
172e-6,
thickness=thickness,
mu=mu,
dist=dist,
poni1=poni1,
poni2=poni2,
mask=mask,
buffer_size=buf,
)
cythick.calc_csr(1)
for i in range(8):
j = 1 << i
print(f"{j:3d} threads: ", end="")
perfs[(j, cythick.buffer_size)] = %timeit -o -n1 -r1 cythick.calc_csr(8, threads=j)
1 threads: 3.55 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
2 threads: 1.93 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
4 threads: 1.1 s ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
8 threads: 685 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
16 threads: 532 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
32 threads: 402 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
64 threads: 347 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
128 threads: 337 ms ± 0 ns per loop (mean ± std. dev. of 1 run, 1 loop each)
fig, ax = subplots(1,2, figsize=(12,6))
t = [i[0] for i in perfs if i[1] == 16]
y16 = [v.best for k,v in perfs.items() if k[1] == 16]
y32 = [v.best for k,v in perfs.items() if k[1] == 32]
p16 = [8e-6*cythick.size/v.best for k,v in perfs.items() if k[1] == 16]
p32 = [8e-6*cythick.size/v.best for k,v in perfs.items() if k[1] == 32]
ax[0].plot(t, y16, label="16 voxel/ray buffer")
ax[0].plot(t, y32, label="32 voxel/ray buffer")
ax[0].set_title("Execution time")
ax[0].set_xlabel("Number of threads")
ax[0].set_ylabel("Runtime (s)")
ax[1].plot(t, p16, label="16 voxel/ray")
ax[1].plot(t, p32, label="32 voxel/ray")
ax[1].set_xlabel("Number of threads")
ax[1].set_ylabel("Millions of rays per second")
ax[1].set_title(cpu)
ax[0].legend();
Conclusion of the raytracing part:#
We are able to simulate the path and the absorption of the photon in the thickness of the detector. Numba/Cython helped substentially to make the raytracing calculation much faster. The signal of each pixel is indeed spread on the neighboors, depending on the position of the PONI and this effect can be inverted using sparse-matrix pseudo-inversion. The MLEM can garanteee that the total signal is conserved and that no pixel gets negative value.
We will now save this sparse matrix to file in order to be able to re-use it in next notebook. But before saving it, it makes sense to spend some time in generating a high quality sparse matrix in throwing thousand rays per pixel in a grid of 64x64 (4 billions rays launched).
%time pre_csr = cythick.calc_csr(128, threads=os.cpu_count())
hq_csr = csr_matrix(pre_csr)
save_npz("csr.npz", hq_csr)
CPU times: user 20min 57s, sys: 961 ms, total: 20min 58s
Wall time: 22.7 s
print(f"Total execution time: {time.perf_counter() - start_time:.3f} s")
Total execution time: 61.854 s